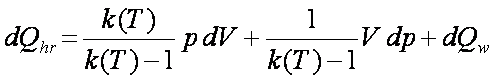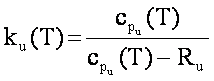Heat Release in Internal Combustion Engines

 

Several models for the evaluation of Gross Heat Release from the internal combustion engine (ICE) are often used in literature. One of these is the First Law − Single Zone Model (FL−SZM), derived from the First Law of Thermodynamics. This model presents a twice advantage: first it describes with accuracy the physic of the phenomenon (charge heat release during the combustion stroke and heat exchange between gas and cylinder wall); second it has a great simplicity in the mathematical formulation. 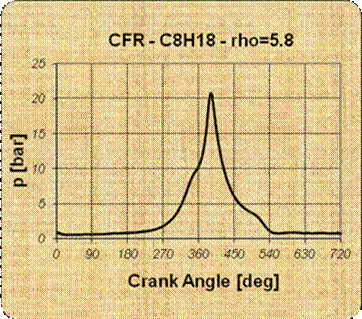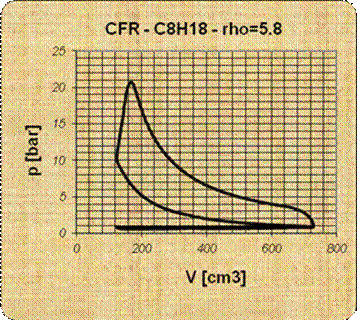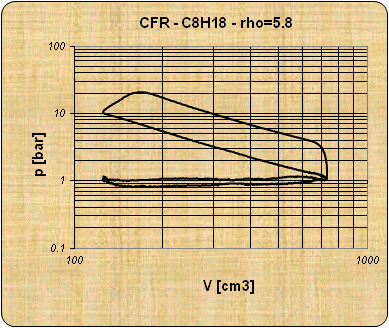The evaluation of Heat Release with the FL−SZM is based on pressure experimental measurements inside the cylinder, and on the assumption of several parameters as the specific heat ratio, wall temperature, polytropic exponent for the motored cycle evaluation, and many others.

 

In order to achieve reliable results, an appropriate equation for k = k(T) (specific heat ratio vs. temperature) which describes the variations of gases thermodynamic properties with the mean temperature inside the cylinder is fundamental.

 

This equation has been calculated by V order Logarithmic Polynomials, VoLPs, fitting experimental gases properties through the least square methods.

 

 

 

 

Step 1: Experimental Measurements

 

 

Engine characteristics

and working conditions

Description

Value

Dimension

Cylinder number

1

-

Compression ratio

3.5 - 18

-

Bore

82.55

mm

Stroke

114.3

mm

Displacement

612

cm3

Cooling system

water recirculation

-

Lubrication system

forced

-

Engine speed

600 ± 6

r/min

Spark advance

13

deg

Fuel

C8H18

-

Equivalence ratio

1

-

External pressure

100050

Pa

External temperature

299

K

Suction air temperature

326

K

Compression ratio

5.8

-

 

 

image001.gif

 

image002.gif

 

 

 

 

 

 

 

Step 2: Heat Release Evaluation

 

 

image013.gif

First Law Single Zone Model – GROSS HEAT RELEASE

 

image014.gif

Specific heat ratio vs. temperature

 

image015.gif

Heat exchanged with the cylinder wall

 

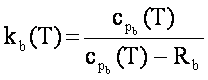
image016.gif               image017.gif

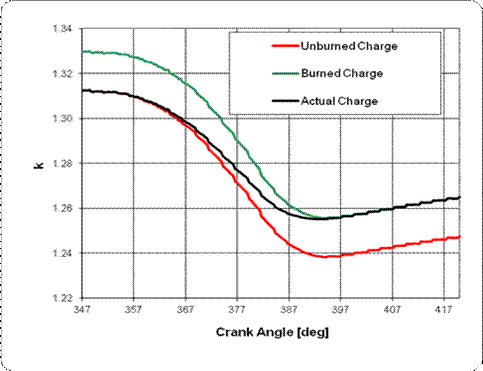
Specific heat ratio for unburned and burned charge

 

cp=specific heat at constant pressure

cp from VoLPs

 

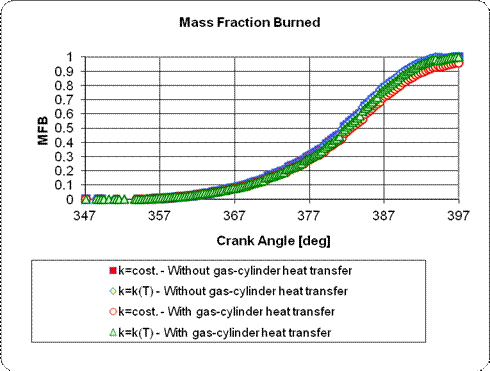
xb=Mass Fraction Burned

 “k” has not a meaningful influence on the MFB, and so

xb can be evaluated from the Gross Heat Release with k = cost. :

 

xb=mb/(mu+mb)=[(Qhr) instantaneous]/[(Qhr) max]

 

 

 

image005.gif

MFB vs Temperature

image024.gif

Specific Heat Ratio vs Crank Angle

 

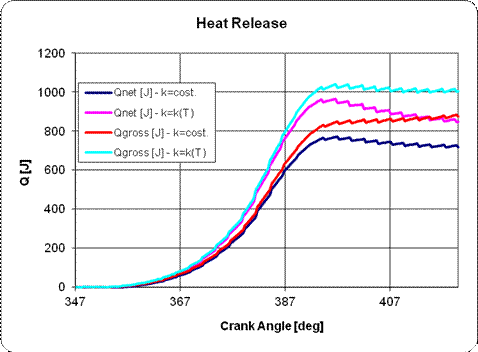
image009.gif

Cumulative Heat Release

 

 

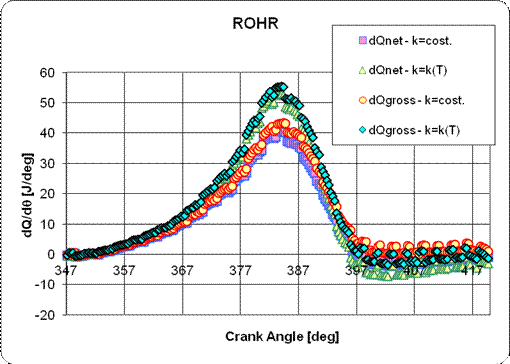
image027.gif

Rate Of Heat Release

 

For more details see the papers reported in Publications.

 

BACK